Физики обнаружили, что обычный лед демонстрирует флексоэлектрические свойства, генерируя электричество при изгибных деформациях. Такое поведение льда ученые объяснили сегнетоэлектрическим фазовым переходом в приповерхностном слое толщиной всего 15-20 нанометров. Работа физиков также указала на возможный вклад флексоэлектричества в разделение зарядов в грозовых облаках. Результаты исследования опубликованы в журнале Nature Physics.
Хоть физики открыли уже 19 кристаллических модификаций водяного льда, характеристики даже самого распространенного обычного льда (он же лед-Ih), изучены далеко не полностью. Например, остается открытым вопрос о его электромеханических свойствах: исследователи неоднократно обращали внимание на связь атмосферного электричества и кристаллов льда в облаках. При этом правила Бернала — Фаулера запрещают льду-Ih генерировать свободные заряды при сжатии или растяжении, поскольку в таком кристалле атомы водорода не демонстрируют структуры дальнего порядка. Другими словами, несмотря на гексагональную решетку, выстроенную атомами кислорода, этот тип льда представляет собой скопление хаотично ориентированных диполей, что противоречит сути пьезоэлектричества. Следовательно, причина появления электрических зарядов должна быть в чем-то другом.
Физики из Испании, Китая и США под руководством Вэнь Синя (Xin Wen) из Университета Сиань Цзяотун предположили, что лед-Ih может генерировать заряды благодаря флексоэлектрическому эффекту — явлению, при котором существует связь между поляризацией материала и градиентом его деформации.
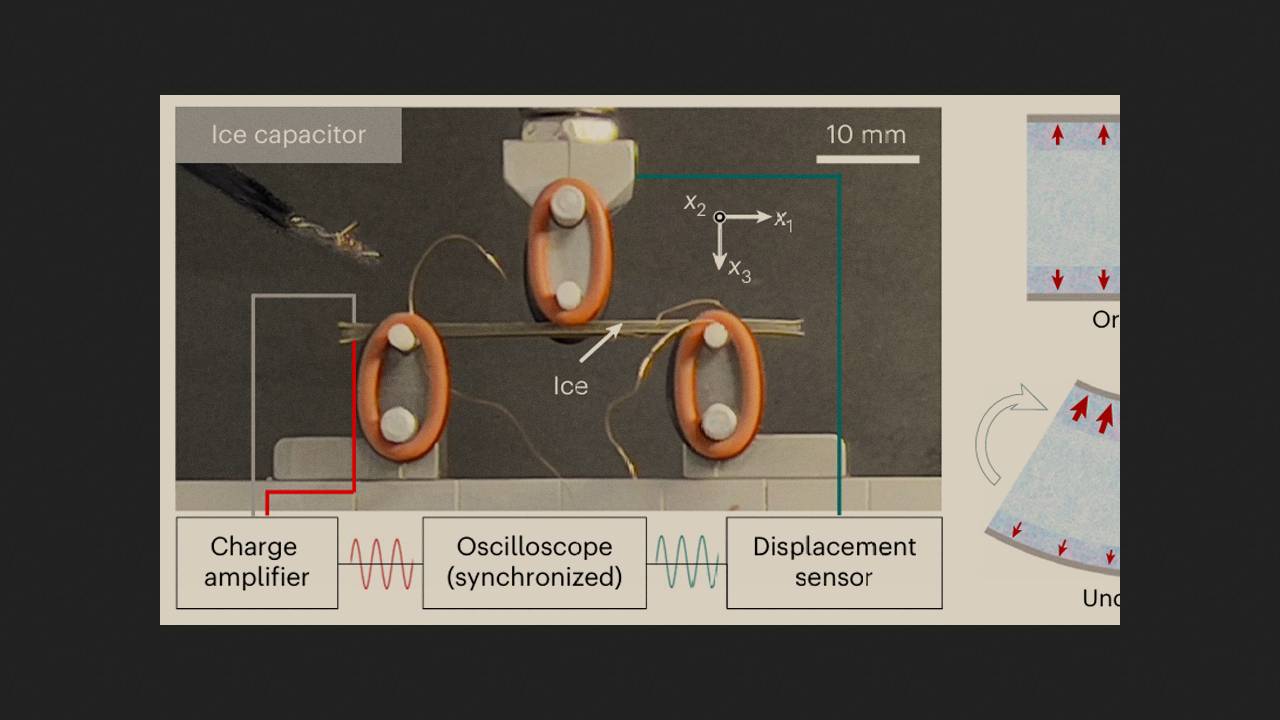
Чтобы проверить свою гипотезу, ученые изготовили конденсаторы из двух покрытых золотом алюминиевых пластин, между которыми заморозили слой сверхчистой воды толщиной примерно два миллиметра. Сначала физики провели пьезоэлектрические измерения, чтобы подтвердить непьезоэлектрическую природу ледяных образцов, а затем использовали динамический механический анализатор и создали в конденсаторах трехточечную изгибную деформацию с максимальным напряжением в 0,006 гигапаскаля, зафиксировав края конденсатора и приложив силу посередине. Такой подход спровоцировал в материале флексоэлектрический отклик, который авторы работы измерили в диапазоне температур от 143 до 273 кельвин.
При температуре выше 248 кельвин флексоэлектричество заметно усилилось, что физики объяснили переходом льда в квазижидкие слои, характерные для тех случаев, когда материал находится в состоянии перед началом плавления, — в таких слоях заключено большое количество подвижных ионов, переносящих заряд. В диапазоне 203-248 кельвин флексоэлектрический коэффициент проявил константные свойства со средневзвешенным значением в 1,14 ± 0,13 нанокулон на метр. Такой результат оказался схожим с диэлектрической керамикой, а коэффициент флексосвязи (флексоэлектрический коэффициент, деленный на диэлектрическую проницаемость), равный 1,29 ± 0,15 вольт, попал в диапазон для собственного флексоэлектричества в твердых телах.
Однако при температуре ниже 203 кельвин флексоэлектрический коэффициент снова вырос, достигнув пика в 7,6 нанокулона на метр при температуре 164,6 ± 1,7 кельвина. Авторы работы отметили, что такая температурная зависимость ранее наблюдалась только в керамических материалах с явными сегнетоэлектрическими свойствами. В итоге физики предположили, что причиной этого флексоэлектрического максимума стал сегнетоэлектрический фазовый переход, ограниченный приповерхностной областью материала. Дополнительным подтверждением гипотезы стала измеренная петля гистерезиса, имевшая форму бабочки, а также вычисленная свободная энергия Гельмгольца, которая показала смещение температуры Кюри к 164,6 кельвина при толщине скин-слоя в 14,6 нанометра (экспериментальная оценка составила 20,3 нанометра).
Помимо этого авторы работы подчеркнули, что их численные оценки объяснили разделение электрических зарядов в грозовых облаках: из-за столкновения крупы с кристалликами льда оба материала деформируются и обмениваются флексоэлектрическими зарядами — крупа становится отрицательно заряженной, а лед положительно. Вместе с тем такая модель очень сильно упрощает все промежуточные процессы, и по мнению физиков, требует дальнейшего уточнения.
О том, как метастабильная вода превратилась в лед-VII и только потом в лед-VI, мы писали ранее.