Фізики спробували визначити масштабованість фазового переходу макроскопічної квантової системи при її вимірюванні, використавши квантовий обчислювач компанії Quantinuum моделі H1 і три різні декодери для передбачення проекції стану. Виявилося, що десятикубітна система перебуває межі між мікро- і макроскопічними масштабами квантових систем. Таким висновком дослідники поділилися у Physical Review X.
При вимірі одиничного квантового об'єкта (наприклад, атомного спина) його суперпозиція станів колапсує в одне конкретне значення спостережуваної величини досить плавно, тобто вимір, який отримує лише малу частину інформації про величину, що спостерігається, ледве обурює квантову систему. Якщо ж виміряти макроскопічну квантову систему (яка в макроскопічних масштабах виявляє квантові властивості), то за деякого критичного значення заходи взаємодії з вимірювальною апаратурою виникає різкий колапс, що проявляється у вигляді фазового переходу (measurement-induced phase transition - MIPT).
З погляду квантової механіки одне з найголовніших питань — де знаходиться межа між мікроскопічною та макроскопічною квантовими системами. Тут якраз і знадобилося б глибоке розуміння процесу MIPT, проте такий колапс системи не може бути змодельований тільки класичними методами, оскільки вимагає постселекції безлічі копій стану з числа обчислювальних ітерацій, що експоненційно зростає.
Уткарш Агравал (Utkarsh Agrawal) з Каліфорнійського університету разом із колегами з Канади та США використовували квантовий пристрій компанії Quantinuum моделі H1 з 20 кубітами на основі іонів ітербію, щоб визначити масштабованість процесу MIPT.
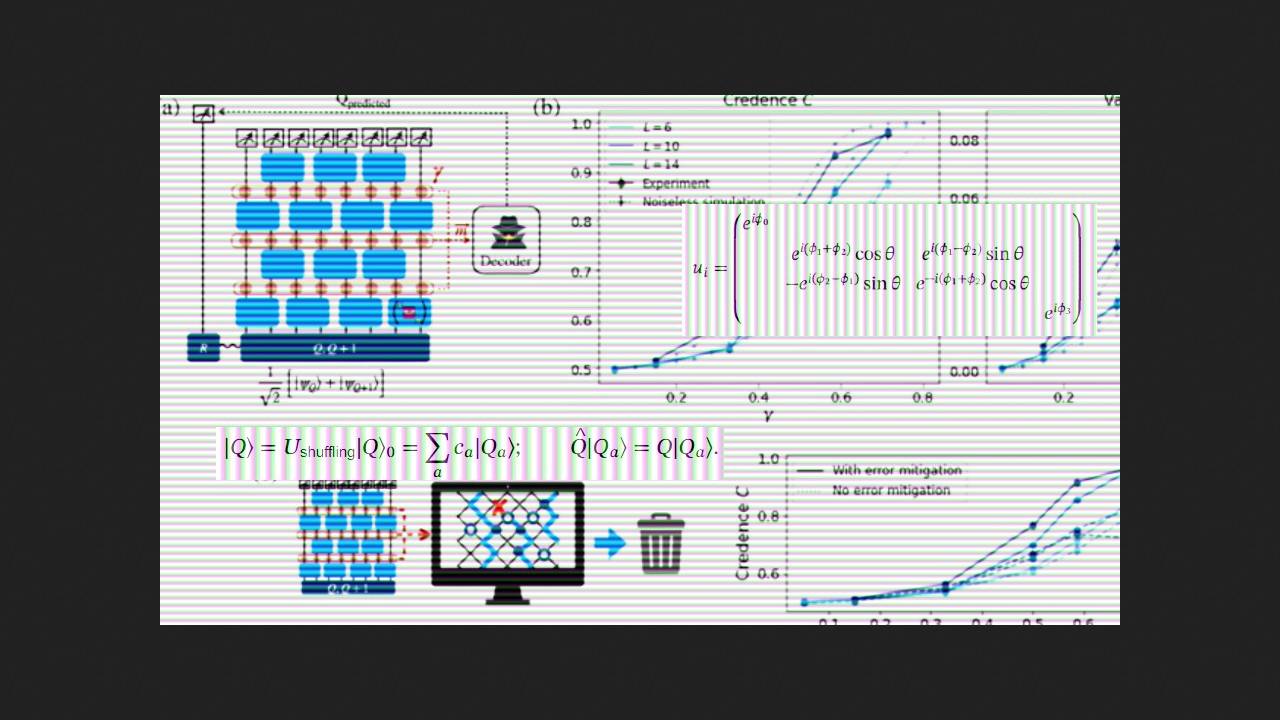
Ученые закодировали начальное состояние кубитов, оставив его неизвестным для воображаемого стороннего наблюдателя — Евы. Сама Ева попыталась предсказать результат коллапса квантовой системы ионов, зная лишь результаты измерений, которые слабо возмутили систему, и используя три различных алгоритма расшифровки. Первый — пост-BQP, который основан на точном моделировании квантовой динамики, но требует экспоненциальных ресурсов даже на квантовом вычислителе, поэтому больше подходит для определения промежуточных результатов. Второй — дешифратор на основе классических методов статистической механики, работающий в узком диапазоне граничных условий для квантовой системы. И наконец, рекуррентный нейросетевой декодер, обученный для того, чтобы узнавать особенности квантовой системы, которые может проигнорировать второй метод расшифровки. С помощью этих алгоритмов Ева оценила вероятность того, что начальное состояние квантовой системы было Q, зная результаты промежуточных измерений M, которые предоставили лишь малую часть информации. Ученые сравнили предсказания Евы, а также их точность, с результатами, полученными на квантовом вычислителе после 300 итераций эксперимента при размере исследуемой системы в 6, 10 и 14 кубитов.
В итоге физики увидели, что при размере системы 14 кубитов все декодеры гораздо лучше предсказали исход эксперимента по сравнению с системой на шести кубитах, а размер системы в 10 кубитов, как предположили ученые, оказался той самой границей между микро- и макроскопическими масштабами. Также исследователи выяснили, что декодер пост-BQP по точности прогнозов значительно превзошел все остальные, а нейросетевой дешифровщик занял промежуточное положение в этом рейтинге, но предсказал результаты без постселекции и, соответственно, дополнительных вычислительных расходов.
Авторы работы отметили, что предложенные ими методы исследования можно легко адаптировать к более широкому кругу моделей квантовых вычислителей. При этом точное определение, какие именно фазовые переходы можно наблюдать с помощью классических или квантовых декодирующих вычислений, остается важной задачей, требующей дополнительного глубокого изучения.
О том, как физики из компании Quantinuum смоделировали неабелевы энионы на квантовых компьютерах, мы писали ранее.