Физики попытались определить масштабируемость фазового перехода макроскопической квантовой системы при ее измерении, использовав квантовый вычислитель компании Quantinuum модели H1 и три различных декодера для предсказания проекции состояния. Оказалось, что десятикубитная система находится на границе между микро- и макроскопическими масштабами квантовых систем. Таким выводом исследователи поделились в Physical Review X.
При измерении единичного квантового объекта (например, атомного спина) его суперпозиция состояний коллапсирует в одно конкретное значение наблюдаемой величины довольно плавно, то есть измерение, которое получает лишь малую часть информации о наблюдаемой величине, едва возмущает квантовую систему. Если же измерить макроскопическую квантовую систему (которая в макроскопических масштабах проявляет квантовые свойства), то при некотором критическом значении меры взаимодействия с измерительной аппаратурой возникает резкий коллапс, проявляющийся в виде фазового перехода (measurement-induced phase transition — MIPT).
С точки зрения квантовой механики один из самых главных вопросов — где находится граница между микроскопической и макроскопической квантовыми системами. Тут как раз и пригодилось бы глубокое понимание процесса MIPT, однако такой коллапс системы не может быть смоделирован только классическими методами, так как требует постселекции множества копий состояния из экспоненциально растущего числа вычислительных итераций.
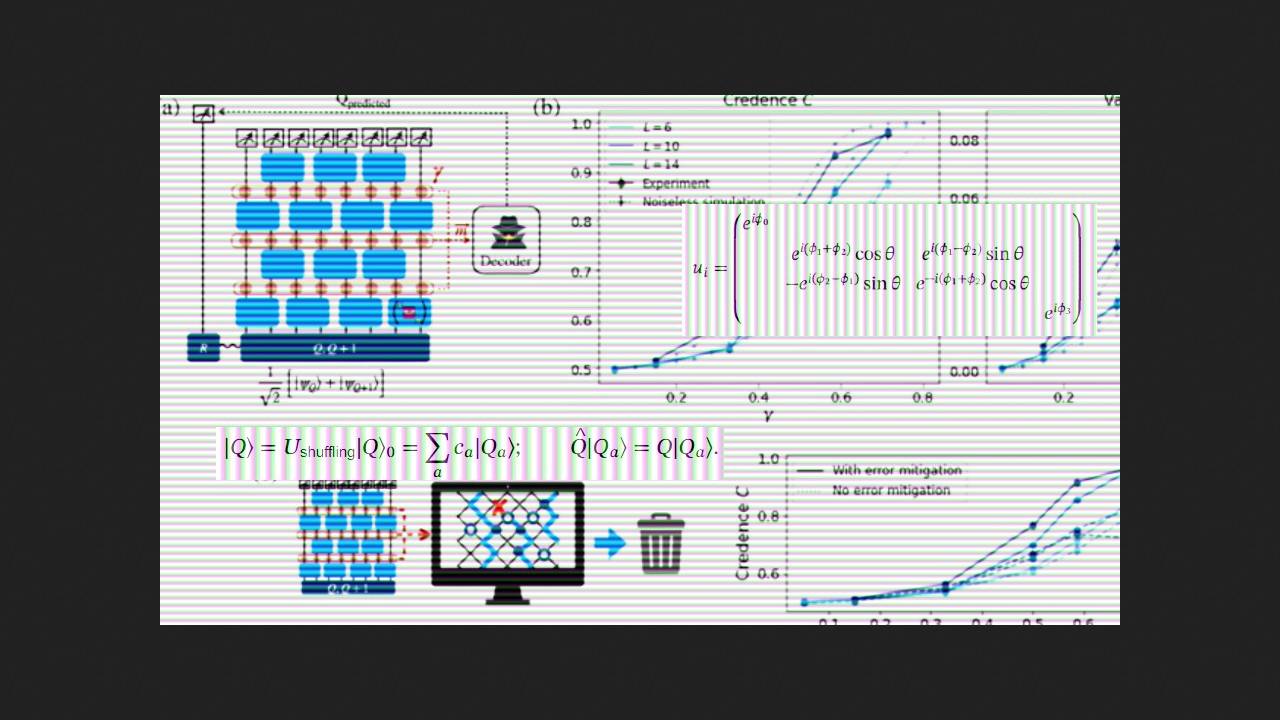
Уткарш Агравал (Utkarsh Agrawal) из Калифорнийского университета вместе с коллегами из Канады и США использовали квантовое устройство компании Quantinuum модели H1 с 20 кубитами на основе ионов иттербия, чтобы определить масштабируемость процесса MIPT.
Ученые закодировали начальное состояние кубитов, оставив его неизвестным для воображаемого стороннего наблюдателя — Евы. Сама Ева попыталась предсказать результат коллапса квантовой системы ионов, зная лишь результаты измерений, которые слабо возмутили систему, и используя три различных алгоритма расшифровки. Первый — пост-BQP, который основан на точном моделировании квантовой динамики, но требует экспоненциальных ресурсов даже на квантовом вычислителе, поэтому больше подходит для определения промежуточных результатов. Второй — дешифратор на основе классических методов статистической механики, работающий в узком диапазоне граничных условий для квантовой системы. И наконец, рекуррентный нейросетевой декодер, обученный для того, чтобы узнавать особенности квантовой системы, которые может проигнорировать второй метод расшифровки. С помощью этих алгоритмов Ева оценила вероятность того, что начальное состояние квантовой системы было Q, зная результаты промежуточных измерений M, которые предоставили лишь малую часть информации. Ученые сравнили предсказания Евы, а также их точность, с результатами, полученными на квантовом вычислителе после 300 итераций эксперимента при размере исследуемой системы в 6, 10 и 14 кубитов.
В итоге физики увидели, что при размере системы 14 кубитов все декодеры гораздо лучше предсказали исход эксперимента по сравнению с системой на шести кубитах, а размер системы в 10 кубитов, как предположили ученые, оказался той самой границей между микро- и макроскопическими масштабами. Также исследователи выяснили, что декодер пост-BQP по точности прогнозов значительно превзошел все остальные, а нейросетевой дешифровщик занял промежуточное положение в этом рейтинге, но предсказал результаты без постселекции и, соответственно, дополнительных вычислительных расходов.
Авторы работы отметили, что предложенные ими методы исследования можно легко адаптировать к более широкому кругу моделей квантовых вычислителей. При этом точное определение, какие именно фазовые переходы можно наблюдать с помощью классических или квантовых декодирующих вычислений, остается важной задачей, требующей дополнительного глубокого изучения.
О том, как физики из компании Quantinuum смоделировали неабелевы энионы на квантовых компьютерах, мы писали ранее.