Physicists attempted to determine the scalability of a macroscopic quantum system's phase transition during its measurement using Quantinuum's H1 quantum computer and three different decoders to predict the state projection. It turned out that the ten-qubit system lies on the boundary between the microscopic and macroscopic scales of quantum systems. The researchers shared this conclusion in Physical Review X.
When measuring a single quantum object (for example, an atomic spin), its superposition of states collapses into a single, specific value of the observable rather smoothly. That is, a measurement that captures only a small portion of the information about the observable barely perturbs the quantum system. However, if we measure a macroscopic quantum system (which exhibits quantum properties on a macroscopic scale), then at a certain critical value of the interaction with the measuring equipment, an abrupt collapse occurs, manifested as a measurement-induced phase transition (MIPT).
From a quantum mechanical perspective, one of the most fundamental questions is where the boundary lies between microscopic and macroscopic quantum systems. This is where a deep understanding of the MIPT process would be useful, but such a system collapse cannot be modeled solely by classical methods, as it requires post-selection of multiple copies of the state from an exponentially growing number of computational iterations.
Utkarsh Agrawal of the University of California, Santa Cruz, and colleagues from Canada and the US used Quantinuum's H1 quantum device, a 20-qubit ytterbium-ion device, to determine the scalability of the MIPT process.
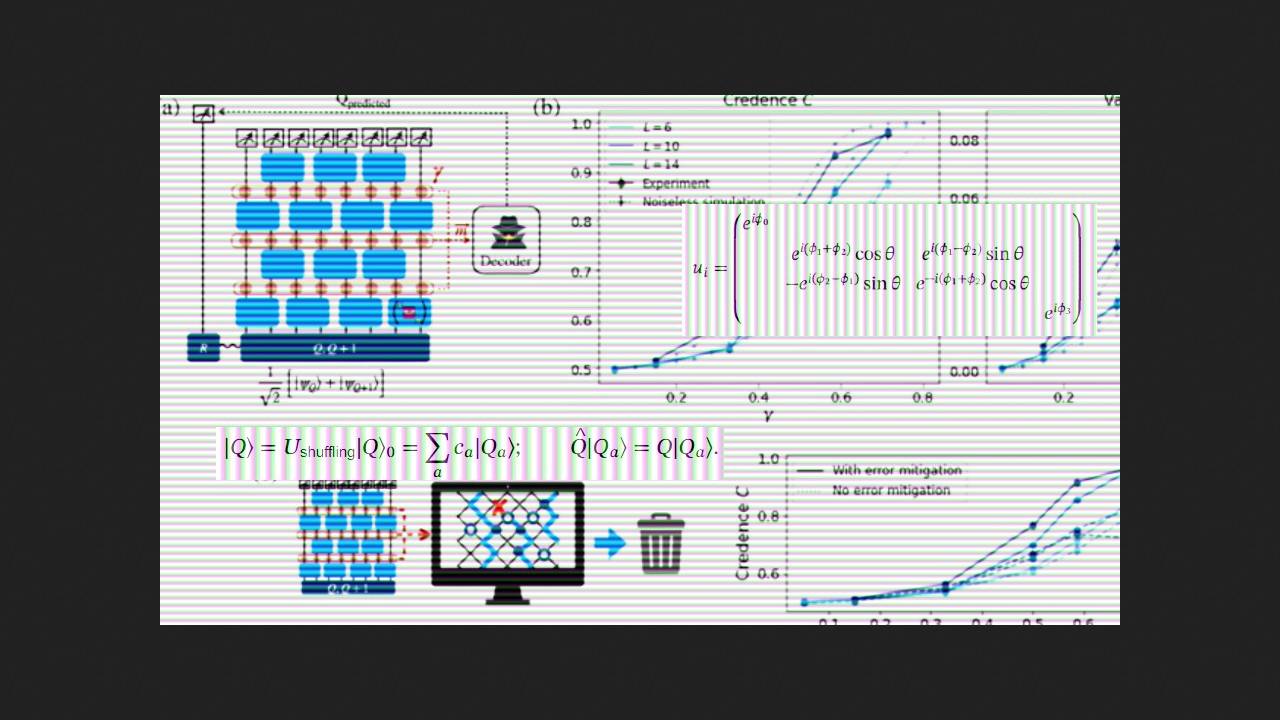
Ученые закодировали начальное состояние кубитов, оставив его неизвестным для воображаемого стороннего наблюдателя — Евы. Сама Ева попыталась предсказать результат коллапса квантовой системы ионов, зная лишь результаты измерений, которые слабо возмутили систему, и используя три различных алгоритма расшифровки. Первый — пост-BQP, который основан на точном моделировании квантовой динамики, но требует экспоненциальных ресурсов даже на квантовом вычислителе, поэтому больше подходит для определения промежуточных результатов. Второй — дешифратор на основе классических методов статистической механики, работающий в узком диапазоне граничных условий для квантовой системы. И наконец, рекуррентный нейросетевой декодер, обученный для того, чтобы узнавать особенности квантовой системы, которые может проигнорировать второй метод расшифровки. С помощью этих алгоритмов Ева оценила вероятность того, что начальное состояние квантовой системы было Q, зная результаты промежуточных измерений M, которые предоставили лишь малую часть информации. Ученые сравнили предсказания Евы, а также их точность, с результатами, полученными на квантовом вычислителе после 300 итераций эксперимента при размере исследуемой системы в 6, 10 и 14 кубитов.
В итоге физики увидели, что при размере системы 14 кубитов все декодеры гораздо лучше предсказали исход эксперимента по сравнению с системой на шести кубитах, а размер системы в 10 кубитов, как предположили ученые, оказался той самой границей между микро- и макроскопическими масштабами. Также исследователи выяснили, что декодер пост-BQP по точности прогнозов значительно превзошел все остальные, а нейросетевой дешифровщик занял промежуточное положение в этом рейтинге, но предсказал результаты без постселекции и, соответственно, дополнительных вычислительных расходов.
Авторы работы отметили, что предложенные ими методы исследования можно легко адаптировать к более широкому кругу моделей квантовых вычислителей. При этом точное определение, какие именно фазовые переходы можно наблюдать с помощью классических или квантовых декодирующих вычислений, остается важной задачей, требующей дополнительного глубокого изучения.
О том, как физики из компании Quantinuum смоделировали неабелевы энионы на квантовых компьютерах, мы писали ранее.