Fizycy próbowali określić skalowalność przejścia fazowego makroskopowego układu kwantowego podczas jego pomiaru, wykorzystując komputer kwantowy H1 firmy Quntinuum oraz trzy różne dekodery do przewidywania projekcji stanu. Okazało się, że układ dziesięciokubitowy leży na granicy między mikroskopową a makroskopową skalą układów kwantowych. Naukowcy podzielili się tym wnioskiem w czasopiśmie Physical Review X.
Podczas pomiaru pojedynczego obiektu kwantowego (na przykład spinu atomowego), superpozycja jego stanów ulega dość płynnej kolapsowi do pojedynczej, określonej wartości obserwowalnej. Oznacza to, że pomiar, który rejestruje jedynie niewielką część informacji o obserwowalnym obiekcie, w niewielkim stopniu zaburza układ kwantowy. Jeśli jednak mierzymy makroskopowy układ kwantowy (który wykazuje właściwości kwantowe w skali makroskopowej), to przy pewnej krytycznej wartości oddziaływania z urządzeniem pomiarowym następuje nagły kolaps, objawiający się przejściem fazowym indukowanym pomiarem (MIPT).
Z perspektywy mechaniki kwantowej jednym z najbardziej fundamentalnych pytań jest to, gdzie leży granica między mikroskopijnymi a makroskopowymi układami kwantowymi. W tym miejscu przydatne byłoby dogłębne zrozumienie procesu MIPT, ale takiego załamania systemu nie da się modelować wyłącznie metodami klasycznymi, ponieważ wymaga to późniejszej selekcji wielu kopii stanu z wykładniczo rosnącej liczby iteracji obliczeniowych.
Utkarsh Agrawal z University of California w Santa Cruz wraz ze współpracownikami z Kanady i USA wykorzystał urządzenie kwantowe H1 firmy Quantinuum, czyli 20-kubitowe urządzenie oparte na jonach iterbu, do określenia skalowalności procesu MIPT.
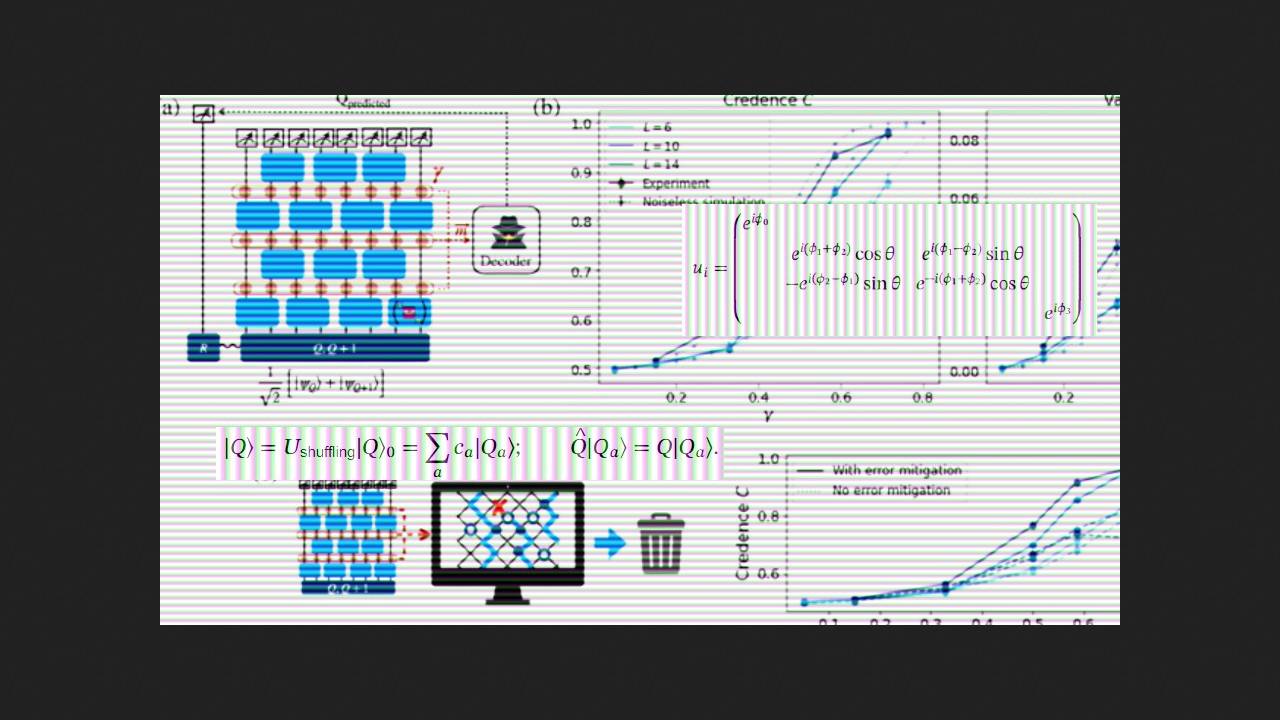
Ученые закодировали начальное состояние кубитов, оставив его неизвестным для воображаемого стороннего наблюдателя — Евы. Сама Ева попыталась предсказать результат коллапса квантовой системы ионов, зная лишь результаты измерений, которые слабо возмутили систему, и используя три различных алгоритма расшифровки. Первый — пост-BQP, который основан на точном моделировании квантовой динамики, но требует экспоненциальных ресурсов даже на квантовом вычислителе, поэтому больше подходит для определения промежуточных результатов. Второй — дешифратор на основе классических методов статистической механики, работающий в узком диапазоне граничных условий для квантовой системы. И наконец, рекуррентный нейросетевой декодер, обученный для того, чтобы узнавать особенности квантовой системы, которые может проигнорировать второй метод расшифровки. С помощью этих алгоритмов Ева оценила вероятность того, что начальное состояние квантовой системы было Q, зная результаты промежуточных измерений M, которые предоставили лишь малую часть информации. Ученые сравнили предсказания Евы, а также их точность, с результатами, полученными на квантовом вычислителе после 300 итераций эксперимента при размере исследуемой системы в 6, 10 и 14 кубитов.
В итоге физики увидели, что при размере системы 14 кубитов все декодеры гораздо лучше предсказали исход эксперимента по сравнению с системой на шести кубитах, а размер системы в 10 кубитов, как предположили ученые, оказался той самой границей между микро- и макроскопическими масштабами. Также исследователи выяснили, что декодер пост-BQP по точности прогнозов значительно превзошел все остальные, а нейросетевой дешифровщик занял промежуточное положение в этом рейтинге, но предсказал результаты без постселекции и, соответственно, дополнительных вычислительных расходов.
Авторы работы отметили, что предложенные ими методы исследования можно легко адаптировать к более широкому кругу моделей квантовых вычислителей. При этом точное определение, какие именно фазовые переходы можно наблюдать с помощью классических или квантовых декодирующих вычислений, остается важной задачей, требующей дополнительного глубокого изучения.
О том, как физики из компании Quantinuum смоделировали неабелевы энионы на квантовых компьютерах, мы писали ранее.